MC dla zespołu kanonicznego

Metoda MC związana jest z zespołami kanonicznymi (o stałej temperaturze).

Jeżeli założymy, że wszystkie stany ponumerujemy zmienną , to prawdopodobieństwo, że układ znajduje się w stanie  jest równe:

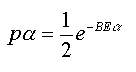gdzie: k_B - stała Bolzmana oraz:

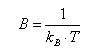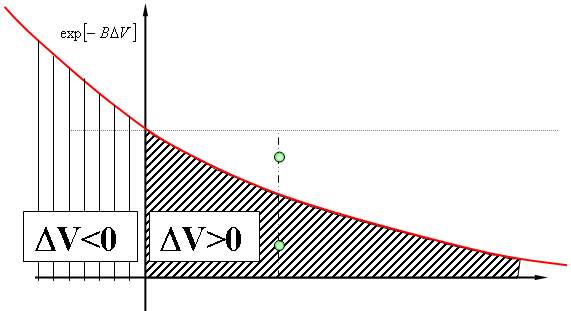
Metoda MC dla zespołu kanonicznego:
1.)Określamy konfigurację początkową.
2.)Generujemy nową konfigurację x'.
3.)Obliczamy zmianę energii deltaE.
4.)Jeżeli deltaE>0, to zaakceptuj nową konfigurację i wróć do kroku 2.
5.)Obliczamy exp(-deltaE/k_BT).
6.)Generujemy liczbę losową R z przedziału [0,1].
7.)Jeżeli R jest mniejsza niż exp(-deltaE/k_BT), to akceptujemy nową konfigurację i wróć do kroku 2.
8.)W przeciwnym przypadku pozostaw starą konfigurację w roli nowej i wróć do kroku 2.

Krok 4.) świadczy o tym, że zawsze akceptujemy nową konfigurację, jeżeli ma ona energię mniejszą niż poprzedzająca. Konfiguracje o podwyższonej energii są akceptowane tylko z prawdopodobieństwem odpowiadającym rozkładowi Boltzmana.