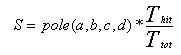Program liczący całkę oznaczoną jako przykład zastosowania metody MC

Jak obliczyć wartość numeryczną całki?

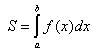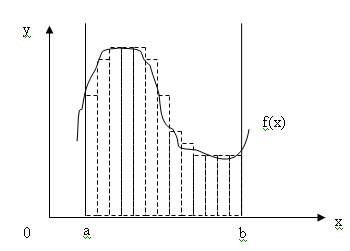
Geometryczna interpretacja całki: całka oznaczona = pole pod krzywą.

Numerycznie Ľz=(a+b)/M), obliczamy f(x_i) dla x₁=a, x₂=a+z, x₃=a+2z, ... , x_M=b-z. Wartość całki jest równa sumie pól prostokątów o bokach: f(x_i) oraz z.

Symulacja metodą MC (1):

Dzielimy przedział <a,b> na M odcinków i przybliżamy całkę wyrażeniem:

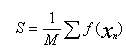Punkty x_n znajdujemy korzystając z generatora liczb pseudolosowych pseudolosowych rozkładzie jednostajnym na przedziale <a,b>.

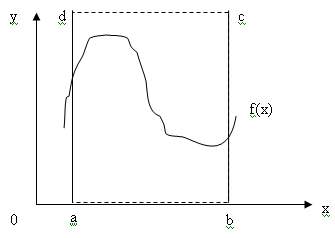
Symulacja metodą MC (2):

Weźmy pod uwagę prostokąt a, b, c, d:

Rzucamy lotkami w prostokąt a, b, c, d.
Niech T_tot - liczba wszystkich rzutów trafionych w prostokąt, T_hit - liczba rzutów, które trafiły pod krzywą.
Wtedy całka wynosi: